すぐるホームページ > 算数 > その他 > 小学生でも理解できる!東大・数学入試問題
小学生でも理解できる!東大・数学入試問題
円周率が3.05より大きいことを証明せよ。
これは,2003年度・東京大学の数学入試問題です。
小学生(中学受験生)ガチの知識で理解できるように工夫しました。
次の「問題1」から「問題4」を解くことによって,自然に解き方がわかってきます。
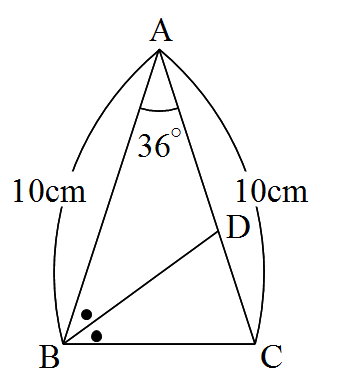
問題1:
右の図の三角形ABCは,角Aが36度で,辺ABと辺ACが10cmの二等辺三角形です。
辺BDは,角Bを二等分する線です。
このとき,辺BCと等しい長さの辺を,すべて答えなさい。

問題1の答え: 辺AD,辺BD
解説:
角B・角Cの大きさは,(180−36)÷2=72(度)。
辺BDは角Bの二等分線なので,角ABDも角CBDも,72÷2=36(度)。
よって,角BDCは,180−(36+72)=72(度)。
したがって,三角形BCDも三角形ABDも,二等辺三角形になります。
よって,辺BC=辺BD,辺BD=辺AD となります。
(解説終わり)

問題1でわかった通り,辺BC=辺BD=辺AD です。それらの長さを ア とし,辺CDの長さを イ とします。
三角形ABCと三角形BCDは相似ですから,
辺BC : 辺CD = 辺AB : 辺BC です。
ア : イ = 10 : ア となり,外項の積と内項の積は等しいので,
ア × ア = イ × 10 という式が成り立ちます。
この式は,あとで使う重要な式なので,「重要式」と名付けておきます。
重要式 ア × ア = イ × 10
では,次の問題に進みましょう。
問題2:
下左図の三角形ABCの,アの長さを使って,下右図のような長方形EFGHを作りました。
この長方形EFGHの面積を求めなさい。必要ならば,
重要式 ア × ア = イ × 10
を使いなさい。

問題2の答え: 100cm2
解説:
下図の長方形EFGHの中の,赤い正方形の面積は,ア × ア です。
また,青い長方形の面積は,イ × 10 です。
重要式 ア × ア = イ × 10 によって,赤い正方形の面積と,青い長方形の面積が等しいのですから,長方形EFGHの赤い正方形を切り取って,かわりに青い長方形をつけ加えても,同じ面積です。
つまり,下図の斜線部分の面積を求めれば良いことになります。
ところで,ア+イは,下左図の辺ACの長さのことですから,10cmです。
よって,斜線部分の面積は,10 × 10 = 100(cm2) になります。(解説終わり)

問題3:
下図の長方形EFGHの面積は100cm2です。このとき,正方形IJKLの面積を求めなさい。

問題3の答え: 125cm2
解説:
長方形EFGHを,ア×アの正方形◎と残りの長方形に分け,さらに長方形部分を☆と★の2つの同じ面積の長方形に分けます。
もちろん,◎と☆と★で100cm2です。
すると,正方形IJKLにも,◎☆★の記号を書くことができ,記号を書いていない部分の面積は,5×5=25(cm2) ですから,正方形IJKLの面積は,100+25=125(cm2) です。

問題4:
右図の正方形IJKLの面積が125cm2のとき,アの長さは6.1cmより長いことを証明しなさい。
問題4の答え:
アの1辺が6.1cmならば,正方形IJKLの1辺は 6.1+5=11.1(cm)なので,面積は 11.1×11.1=123.21(cm2) となるが,実際は125(cm2)なので,アは6.1cmより長い。
問題:
円周率が3.05より大きいことを証明せよ。

証明: 問題4でわかった通り,アの長さは6.1cmより長いです。
ということは,二等辺三角形ABCを10個並べた正十角形のまわりの長さは,6.1×10=61(cm)より長いことになります。

半径10cmの円の円周も,61cmより長いです。
「円周=直径×円周率」の,直径が 10×2=20(cm)のときに,円周は61cmより長いので,円周率は,61÷20=3.05 より大きいことが証明できました。
(証明終わり)
Copyright (C) 1996- Suguru Corporation. All Rights Reserved.












