| すぐるホームページ・トップ > 学習教材 > 算数教材 > すぐるの算数カルチャー講座 > ラムゼーゲーム > ルールを変えると先手が必ず勝つ理由 | |
| ルールを変えると先手が必ず勝つ理由 | |
|
このページでは,ラムゼーゲームのルールを, 自分の色の三角形を作った方が,勝ちになる。 というルールに変えたとすると, 先手が必ず勝つ。 ということになる理由を考えていきます。
まず,先手が(どこでも構わないので)適当に,右図のように赤線を引いたとします。 それに対して,後手の線の引き方は2種類あります。 1.赤線の端から青線を引く。(図1) 2.赤線とは関係なく,青線を引く。(図2)
自分の色の三角形を作った方が勝ち,というルールなら,どちらの場合にも,必ず先手が勝ってしまうのです。
1.赤線の端から青線を引いた場合  赤線の一方の端からは,青線が引いてあります。(右図の緑の点)
赤線の一方の端からは,青線が引いてあります。(右図の緑の点)
また,赤も青も引かれていない点が,3個あります。 右の図では,1番の点にめがけて赤線を引きました。 さあ,次に引くのは後手の青線です。
青線はどこに引かなければならないか,もうわかりましたね。
先手の赤は,またまた緑丸の点から,赤も青も引かれていない点に,赤線を引きます。 右図の場合は,2番の点にめがけて赤線を引いてあります。
この状態では,もう赤の勝ちであることがわかりますか?
後手(青)がアに引かなかったら,先手(赤)はアに引けば赤の勝ちです。
どちらにしろ,必ず先手(赤)が勝つわけですね。
2.赤線とは関係なく,青線を引いた場合 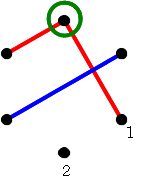 赤も青も引かれていない点が,2個あります。
赤も青も引かれていない点が,2個あります。
そのどちらかの点から,すでに引いてある赤線のどちらかの端まで,赤線を引きます。 先手の赤は,またまた緑丸の点から,赤も青も引かれていない点に,赤線を引きます。 右図のように,2番の点にめがけて赤線を引くわけです。
この状態では,もう赤の勝ちであることがわかりますか?
後手(青)がアに引かなかったら,先手(赤)はアに引けば赤の勝ちです。
どちらにしろ,必ず先手(赤)が勝つわけですね。
(証明終)
|
↓ラムゼーゲームの存在を,この本で知りました。
|
 先手は赤,後手は青の線を引くことにします。
先手は赤,後手は青の線を引くことにします。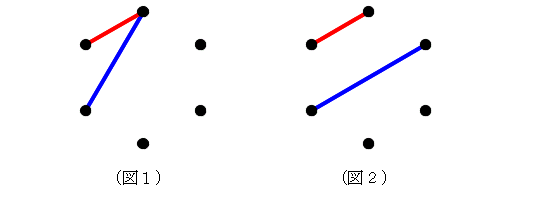
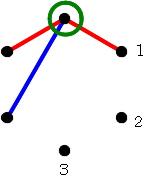 緑丸の点から,赤も青も引かれていない点のどれかに,赤線を引きます。
緑丸の点から,赤も青も引かれていない点のどれかに,赤線を引きます。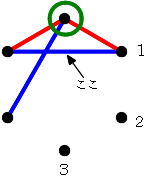 そうです。後手(青)は,右の図の「ここ」のところに線を引かないと,負けてしまいますね。
そうです。後手(青)は,右の図の「ここ」のところに線を引かないと,負けてしまいますね。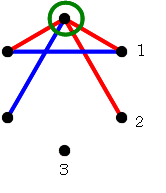 でも,もう青に勝ち目はないのです。
でも,もう青に勝ち目はないのです。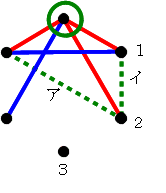 次の番である後手(青)が,右図のアに青線を引いたら,先手(赤)はイに引けば赤の勝ちです。
次の番である後手(青)が,右図のアに青線を引いたら,先手(赤)はイに引けば赤の勝ちです。 すると,後手(青)は,右の図の「ここ」のところに線を引かないと,負けてしまいますね。
すると,後手(青)は,右の図の「ここ」のところに線を引かないと,負けてしまいますね。 でも,もう青に勝ち目はないのです。
でも,もう青に勝ち目はないのです。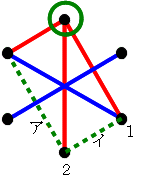 次の番である後手(青)が,右図のアに青線を引いたら,先手(赤)はイに引けば赤の勝ちです。
次の番である後手(青)が,右図のアに青線を引いたら,先手(赤)はイに引けば赤の勝ちです。